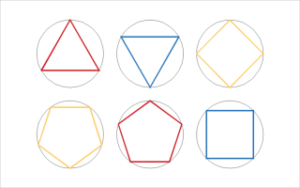
Ringjoone jaotamine võrdseteks osadeks

Ringjoone jaotamine võrdseteks osadeks on geomeetriliste konstruktsioonide põhioskus. Joonestamisvilumuse ja graafilise lahendamisoskuse arendamiseks on hea, kui oskame kasutada erinevaid viise ja töövahendeid.

Jaotuspunktide võrdsed vahekaugused ringjoonel saame arvutada, kui:

  • jagame ringjoone pikkuse soovitud jaotuspunktide arvuga n ja saame teada kaarelõikude pikkuse jaotuspunktide vahel. Otse mööda kõverjoont tippude vahekauguste mõõtmiseks ei ole meil üldjuhul kasutada käepäraseid vahendeid;
  • jagame täisringi suuruse ehk 360° soovitud jaotuspunktide arvuga n ja saame teada kesknurga suuruse. Kesknurka määravad raadiused eraldavad ringjoonest ühe osa, 1/n suuruse tüki. Raadiused märgivad ringjoonel 2 jaotuspunkti – need ühendame kõõluga. Tekkinud kolmnurk on korrapärase hulknurga määrav kolmnurk.

Manuaalselt

Vaatame, kuidas jaotada ringjoon võrdseteks osadeks. Jaotamisel võime kasutada:

  • malli, millega mõõdame kesknurki (loe lisa malli kasutamise kohta),
  • sirklit ja kahte joonlauda, millega konstrueerime ringjoone sisse korrapärase hulknurga.

Käsitleme konstrueerimist sirkli, joonlaua ja malliga. Sirklina võime kasutada nii joon- kui mõõtsirklit. Esimest eelkõige joone tõmbamiseks, teist aga pikkuste kontrollimiseks ja joonisele märkimiseks (kerge vajutus nõelaga jätab paberile vao). Joonlaudadest vähemalt üks peab olema kolmnurkjoonlaud. Teine võib olla ristkülikjoonlaud. Kuid suurepärased kasutada on ka kaks kolmnurkjoonlauda koos. Kolmnurkjoonlaud on abiks ringjoone teineteisega ristuvate telgjoonte joonestamisel.

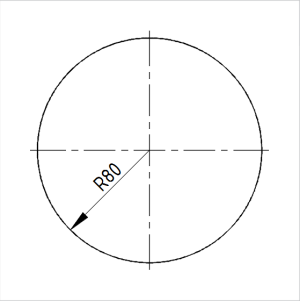Joonisel on kujutatud ringjoon, mille keskpunkti läbivad telgjooned ulatuvad ringjoonest üle võrdse pikkuse võrra. Lisatud on ringi raadiusmõõt R80.

Joonis. Ringjoone kujutis ja ringi suurus

 Korrektse joonise saame, kui kujutame ringjoont graafiliselt õigesti:

  • Ringjoone keskpunkti tähistame vertikaalse ja horisontaalse telgjoone lõikumisena. Telgjoon on kitsas kriips-punkt-joon. (vt joonis)
  • Keskpunkti täpseks tähistamiseks on oluline, et ringi keskel ristuvad vertikaalse ja horisontaalse telgjoone pikad kriipsud (vt joonis).
  • Telgjooned joonestame kõikides telgpunktides üle ringjoone võrdse pikkuse võrra (telgpunkt = ring- ja telgjoone lõikepunkt). Üleulatuva osa pikkus on 3-5 mm.
  • Ringjoone joonestame ühtlase laiusega pideva kontrastse joonega (vastavalt kas kitsa või laiaga, oleneb vajadusest).

Nutikas on õppida ringjoont jaotama kolmeks, neljaks ja viieks võrdseks osaks. Need on nn põhikonstruktsioonid.

Kui soovime aga ringjoont jaotada näiteks kuueks, siis sisuliselt jaotame ringjoone kaks korda kolmeks osaks, nii et näiteks ühe kolmnurga tipp asub vertikaalteljel ringjoone ülemises telgpunktis ja teise kolmnurga tipp samal teljel ringjoone alumises telgpunktis.

Kirjeldatud viisil, kus ühesuguste hulknurkade asendit on ringjoone sees üksteise suhtes sümmeetriliselt muudetud, saame ringjoone jaotada:

  • kaheksaks (2 korda 4-ks),
  • kümneks (2 korda 5-ks) ja
  • kaheteistkümneks (4 korda 3-ks) jne.

Sirkli ja joonlauaga saame graafiliselt täpselt tuletada korrapäraseid kõõlhulknurki, mille tippude arv on 3, 4 või nende paarsiarvuline kordne.

Manuaalsel ringjoone jaotamisel paarituks arvuks võrdseks osaks tekib graafikas mõnel juhul väike viga. Pliiatsijoonega saame vea küll peita, kuid tegelikult ei ole selline joonis täpne, sest kõikide kõõllõikude pikkused ei ole võrdsed. Töö tegemisel tuleb meil selle omapäraga arvestada.

Oskuse ja vilumuse kujundamiseks joonestame paberile mõned ringjooned ja jaotame neist igaühe  eri arvuks võrdseteks osadeks.

Lahenduspõhimõte

Ringjoone võrdseteks osadeks jaotamiseks:

  1. joonestame ringjoone jaotamiseks vajalikud konstruktsioonjooned,
  2. kontrollime mõõtsirkliga üle, et ringjoonele tuletatud jaotuspunktid on võrdsete vahekaugustega,
  3. ühendame jaotuspunktid kõõludega.

Tegevus ise on lihtne, kuid nõuab keskendumist, tähelepanu ja graafilist täpsust.

Oluline on panna sirkli teravik punkti täpselt. Kui kasutame kontrollimiseks joonsirklit, peab vaatama, millise kohaga täpselt sirkli grafiitots joone tõmbab või mõõdu võtab. Samuti on oluline, et konstruktsioonjoon läbiks punkti täpselt, mitte ei läheks sellest ülevalt ega altpoolt.

Punkt võib olla tähistatud:

  • väikese ringikesega – sel juhul on täpne punkt ringikese keskpunkt,
  • joonte lõikumisega – sel juhul on täpne punkt joonte lõikepunkt.

Tähelepanu!
(1) Käesolevas õppematerjalis tähistavad kaldkriipsud joontel ringjoone võrdsete pikkustega kõõle.
(2) Kui kontrollmõõtmisel ei ole kõõlude pikkused võrdsed, tuleb lahendus parandada, kontrollida ja alles seejärel töö lõplikult vormistada.

(1) Ringjoone jaotamine kolmeks võrdseks osaks

Näide 1.1. Korrapärase kõõlkolmnurga üks tipp ühtib ringjoone telgpunktiga
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

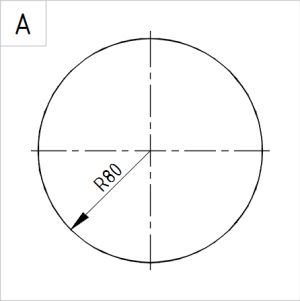Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

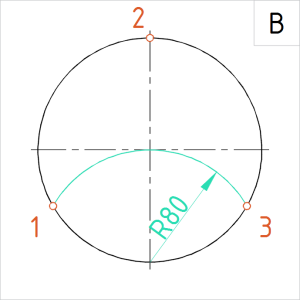Joonis. Ringjoone jaotamine 3 võrdseks osaks (üks jaotuspunkt on ringjoone ülemises telgpunktis)

 B. Vertikaaltelje alumisest telgpunktist joonestame kaare raadiusega 80 mm (vt joonis), mis lõikub ringjoonega kahes punktis (1 ja 3). Need punktid koos ülemises telgpunktis asuva punktiga 2, jaotavadki ringjoone kolmeks võrdseks osaks.

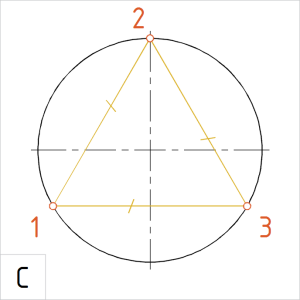Joonis. Korrapärane kõõlkolmnurk

 C. Võtame sirklisse kahe järjestikuse jaotuspunktiga määratud kõõlu pikkuse ja mõõdame kontrolliks üle kõigi ülejäänud kõõlude pikkused. Need pikkused peavad olema võrdsed pikkustega.

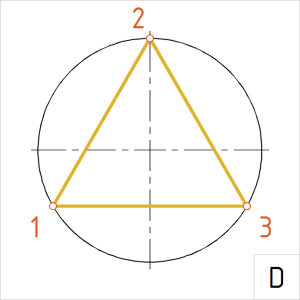Joonis. Kõõlkolmnurk

 D. Korrastame joonise ja joonestame kõõlud üle laijoonega. (PS. Teljega paralleelse kõõlu korrastamisel on korrektne kasutada paralleellüket.)
(1) Iseseisev harjutus:

Joonesta ringjoon (R > 29 mm) ja selle sisse korrapärane kõõlkolmnurk nii, et kolmnurga üks tipp asub ringjoone telgpunktis horisontaalteljel vasakul.
Näide 1.2. Korrapärase kõõlkolmnurga ükski tipp ei ühti ringjoone telgpunktiga
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

Joonis. Ringjoon R80

 Kuidas konstrueerida korrapärast kõõlkolmnurka, kui soovime kolmnurga tippe telgpunktide suhtes nihutada?

A. Joonestame ringjoone raadiusega 80 mm.

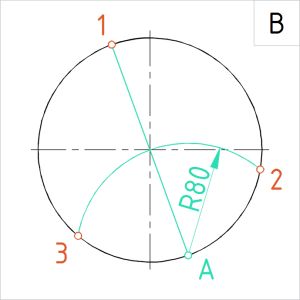Joonis. Ringjoone jaotamine 3 võrdseks osaks (ükski jaotuspunkt ei asu ringjoone telgpunktis)

 B. Valime ringjoonel kolmnurga üheks tipuks vabalt ühe punkt 1. Ühendame punkti 1 ringjoone keskpunktiga ja pikendame joone ringi diameetriks. Tähistame diameetri teise otspunkti A -ga. Joonestame punktist A kaare ringi raadiusega 80 mm. Kaar lõikub ringjoonega kahes punktis (2 ja 3). Nüüd on ringjoonel kolm võrdse vahega jaotuspunkti.

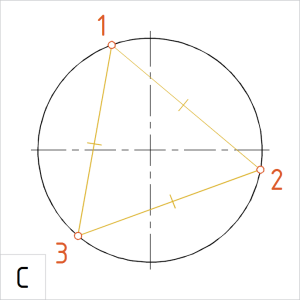Joonis. Korrapärane kõõlkolmnurk

 C. Võtame sirklisse kahe järjestikuse jaotuspunkti vahemiku (kõõlu) ja kontrolliks mõõdame üle kõik kõõlud. Nende pikkused peavad olema võrdsed. Kui pikkused on võrdsed, ühendame jaotuspunktid kõõludega.

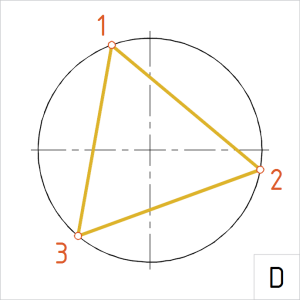Joonis. Kõõlkolmnurk

 D. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.
(2) Iseseisev harjutus:

Joonesta ringjoon (R > 29 mm) ja selle sisse korrapärane kõõlkolmnurk nii, et kolmnurga üks tipp asub ringjoonel telgjoontest tekkinud nurga poolitajal.
Näide 1.3. Korrapärase kõõlkolmnurga konstrueerimine ringjoone kesknurga abil
Ringjoone jaotamiseks kasutame malli ja joonlauda.

Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

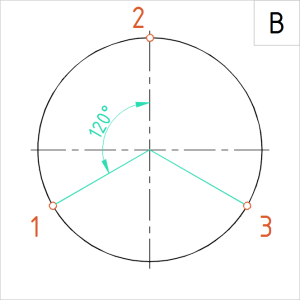Joonis. Ringjoone täispöörde jaotamine 3 võrdseks osaks

 B. Ringjoon moodustab täispöördel 360-kraadise nurga. Kui jaotame täispöörde kolmeks, saame iga kesknurga suuruseks 120°.

PS. Kui meil on kasutada kaks täisnurkset 30° ja 60° teravnurkade joonestuskolmnurka, saame jaotussirge joonestada joonlaudade 60° nurkade järjestikku paigutamisega. 60°+60°=120°.

Nüüd tuleb punktid järjestikku kõõludega ühendada pideva laijoonega.

(2) Ringjoone jaotamine neljaks võrdseks osaks

Näide 2.1. Korrapärase kõõlnelinurga kõik tipud ühtivad ringjoone telgpunktidega
Ringjoone jaotamiseks kasutame joonlauda.

Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

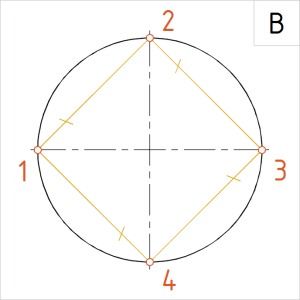Joonis. Korrapärane kõõlnelinurk

 B. Vertikaalne ja horisontaalne telg lõikuvad ringjoonega ja märgivad telgpunktid 1, 2, 3, 4, mis jaotavadki ringjoone neljaks võrdseks osaks. Võtame sirklisse kahe järjestikuse jaotuspunkti vahemiku (kõõlu) ja mõõdame kontrolliks üle kõik vahemikud. Nende pikkused peavad olema võrdsed. Kui pikkused on võrdsed, ühendame jaotuspunktid kõõludega.
Tähelepanu! Kõõlude pikkused ei ole võrdsed, kui telgjooned ei moodusta omavahel täisnurka või ringjoon ei ole joonestatud püsiva raadiusega. Vead tuleb parandada.

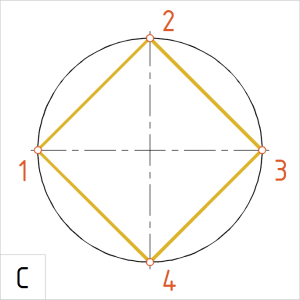Joonis. Kõõlnelinurk

 C. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.
Näide 2.2. Korrapärase kõõlnelinurga tipud asuvad ringjoone telgedevahelise nurga poolitajatel
Ringjoone jaotamiseks kasutame:

  • (I) kahte joonlauda; Tähelepanu! Üks neist peab olema 45-kraadiste teravnurkadega täisnurkne kolmnurkjoonlaud,
  • (II) sirklit ja joonlauda.

Joonis. Ringjoon R80

 Kuidas jaotada ringjoont juhul, kui soovime, et kõõlud on telgjoontega paralleelsed?

A. Joonestame ringjoone raadiusega 80 mm.

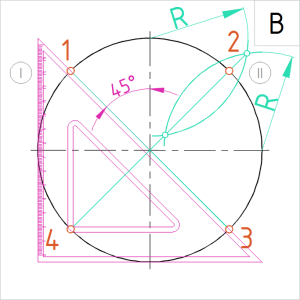Joonis. Ringjoone jaotamine 4 võrdseks osaks, kasutades telgjoonest moodustunud nurkade poolitamist

 B. Konstrueerida saame kahel viisil:

  • (I) 45-kraadiste teravnurkadega kolmnurkjoonlaua abil,
  • (II) sirkliga konstrueeritud nurga poolitaja abil.

(I) Vajame oskust teha kolmnurkjoonlauaga paralleellüket.
Kolmnurkjoonlaua ühe kaatetserva joondame paralleelseks ringjoone vertikaalsele teljele. Asetame kolmnurga alumisele kaatetservale toeks teise joonlaua ja hoiame seda vasaku käe sõrmedega paigal. Nüüd nihutame kolmnurkjoonlaua mööda tugijoonlaua serva vasakule, kuni kolmnurkjoonlaua hüpotenuusserv läbib ringjoone keskpunkti. Joonestame telgjoontest moodustunud 90-kraadistesse nurkadesse nurga poolitaja. Selliselt tuletame jaotuspunktide 1 ja 3 asukohad. (Hoiame tugijoonlauda paigal, pöörame kolmnurga ümber, asetame tugijoonlauale, nihutame hüpotenuusserva telgede lõikepunkti ja poolitame ka kõrvalolevad sektorid.)

(II) Nurga poolitamine sirkli ja joonlaua abil.
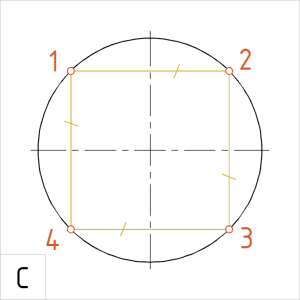Jaotame vertikaalsest teljest paremale jääva nurga pooleks. Selleks joonestame ringjoone vertikaalse ja horisontaalse telje telgpunktidest vabalt valitud raadiusega R kaared. Kaared peavad lõikuma. Kaarte lõikepunktid ühendame ringjoone keskpunktiga ja pikendame kuni ringjooneni teisel pool keskpunkti. Oleme tuletanud jaotuspunktid 2 ja 4. (Jaotame ka kõrvalolevad sektorid.)

Joonis. Korrapärane kõõlnelinurk

 C. Võtame sirklisse kahe järjestikuse jaotuspunkti vahemiku (kõõlu) ja kontrolliks mõõdame üle kõikide kõõlude pikkused. Need peavad olema võrdsed. Kui pikkused on võrdsed, ühendame jaotuspunktid kõõludega.

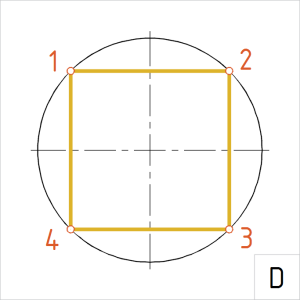Joonis. Kõõlnelinurk

 D. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.

(3) Ringjoone jaotamine viieks võrdseks osaks

Näide 3.1. Korrapärase kõõlviisnurga külje pikkuse tuletamine (variant 1)
Ringjoone jaotamisel kasutame sirklit ja joonlauda.

Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

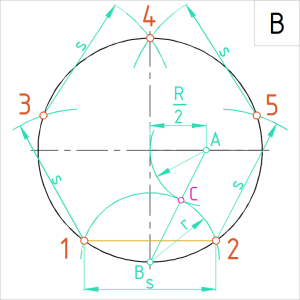Joonis. Ringjoone jaotamine 5 võrdseks osaks, lahutades lõigust AB pool raadiuslõiku

 B. Ringjoonest ühe viiendiku eraldamine. Neli etappi:

(1) Poolitame ringjoone horisontaalsel teljel raadiuslõigu keskpunktist paremal. Tähistame keskpunkti A-ga.

(2) Ühendame raadiuslõigu keskpunkti A ringjoone vertikaaltelje alumise telgpunktiga B.

(3) Lahutame sirglõigust AB pool raadiuslõiku. Selleks joonestame raadiuslõigu keskpunktist A kaare raadiusega R/2 . Kaare lõikepunkti sirgel AB tähistame punktiga C.

(4) Joonestame raadiusega BC  kaare ringjoone alumisest telgpunktist B. Kaar lõikub ringjoonega kahes punktis – 1 ja 2 ning nende punktide vahemik eraldab ringjoonest 1/5.

Võtame sirklisse kõõlu 12 ning joonestame selle pikkusega punktidest 1 ja 2 kaared lõikuma ringjoonega. Saame punktid 3 ja 5. Järgmisena joonestame sama kõõlu pikkusega kaared ka  punktidest 3 ja 5, mis peavad omavahel lõikuma täpselt ringjoone ülemises telgpunktis.

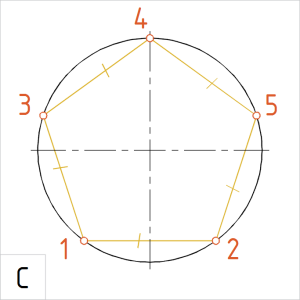Joonis. Korrapärane kõõlviisnurk

 C. Kontrolliks mõõdame üle kõigi kõõlude pikkused. Nad  peavad olema võrdsed. Ühendame jaotuspunktid kõõludega.

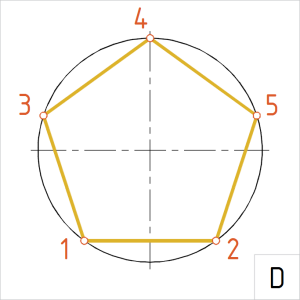Joonis. Kõõlviisnurk

 D. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.
Näide 3.2. Korrapärase kõõlviisnurga telgsümmeetriliste tippude tuletamine
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

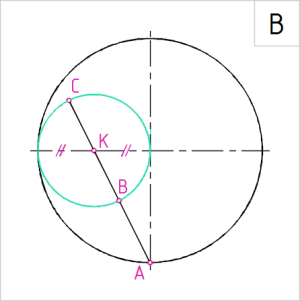Joonis. On tehtud kõik vajalikud konstruktsioonid

 B. Teeme lahendamiseks vajalikud konstruktsioonid.

(1) Poolitame ringjoone raadiuslõigu horisontaalsel teljel keskpunktist vasakul – punkt K. (Kaldsed paariskriipsud väljendavad poollõikude võrdseid pikkusi.)

(2) Raadiuslõigu keskpunktist K joonestame raadiusega R/2 ringjoone, mis läbib ringjoone telgpunkti horisontaalteljel vasakul ja paremal antud ringjoone keskpunkti (telgede lõikepunkti).

(3) Joonestame ringjoone alumisest telgpunktist A sirge läbi punkti K ning pikendame sirget edasi kuni väikese ringjooneni. Sirge lõikepunktid väikesel ringjoonel tähistame B ja C -ga.

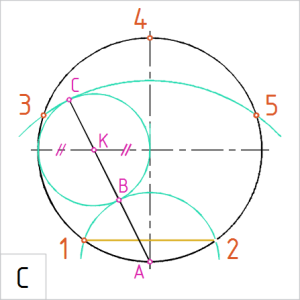Joonis. Raadiusega AB joonestatud kaar eraldab ringjoonest 1/5 – tipud 1 ja 2. Kaar AC tuletab ringjoonel viisnurga tipud 3 ja 5.

 C. Tuletame kõõlviisnurga tipud.

(1) Joonestame punktist A raadiusega AB  kaare. Kaare lõikepunktid ringjoonel on hulknurga tipud 1 ja 2.

(2) Joonestame punktist A raadiusega AC  kaare lõikuma antud ringjoonega. Kaare lõikepunktid ringjoonel on tipud 3 ja 5.

(3) Ringjoone ülemise telgpunkti märgime tähisega 4.

(4) Kontrollime, et kõõlude pikkused on võrdsed ja punktipaarid 1  ja 2  ning 3  ja 5  telgsümmeetrilised.

(5) Ühendame tipud järjestikku kitsa pidevjoonega.

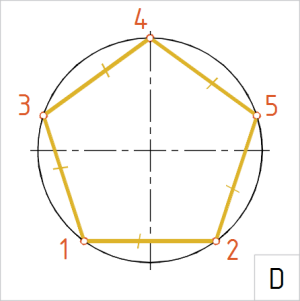Joonis. Korrapärane kõõlviisnurk

 D. Korrastame joonise ning joonestame kõõlud üle pideva laijoonega.
Näide 3.3. Korrapärase kõõlviisnurga külje pikkuse tuletamine (variant 2)
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

Joonis. Ringjoon R80

 A. Joonestame ringjoone raadiusega 80 mm.

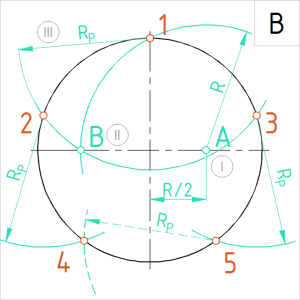Joonis. Ringjoone jaotamine 5 võrdseks osaks lõiguga B1

 B. Konstruktsioon koosneb neljast sammust.

(1) Poolitame ringjoone raadiuslõigu horisontaalsel teljel keskpunktist paremal – punkt A.

(2) Tähistame ülemise telgpunkti tähisega 1 ja joonestame kaare raadiusega A1 lõikuma horisontaalse teljega vasakul – punkt B.

(3) Joonestame punktist 1 kaare raadiusega B1 . Kaar märgib ringjoonega lõikudes jaotuspunktid 2 ja 3.

(4) Punktidest 2 ja 3 joonestame omakorda kaared raadiusega B1 . Kaared märgivad ringjoonel punktid 4 ja 5.

Nüüd on ringjoonel viis võrdse vahega jaotuspunkti.

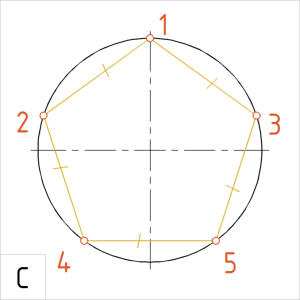Joonis. Korrapärane kõõlviisnurk

 C. Kontrolliks võtame sirklisse kõõlu 12  ja mõõdame üle kõigi kõõlude pikkused. Nad peavad olema võrdsed. Ühendame jaotuspunktid kõõludega.

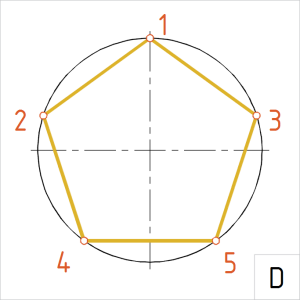Joonis. Kõõlviisnurk

 D. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.

(4) Ringjoone jaotamine kuueks võrdseks osaks

Näide 4.1. Korrapärane kõõlkuusnurk kahe korrapärase kõõlkolmnurga konstrueerimisega; kolmnurkade tipud asuvad ringjoone alumises ja ülemises telgpunktis vertikaalteljel.
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

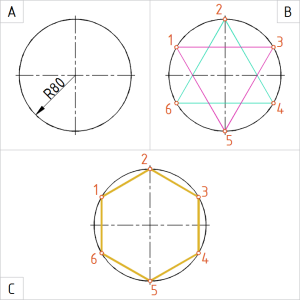Joonis. Ringjoone 6 võrdseks osaks jaotamisel konstrueerime ringjoone sisse kaks korrapärast kõõlkolmnurka, millede tipud 2 ja 5 asuvad ringjoone telgpunktides vertikaalteljel

 A. Joonestame ringjoone raadiusega 80 mm.
B. Jaotame ringjoone kaks korda kolmeks:

  • kolmnurga 246 saamiseks joonestame kaare ringjoone alumisest telgpunktist vertikaalteljel raadiusega R80; kaare ja ringjoone lõikepunktid määravad punktid 6 ja 4 (vt ringjoone jaotamine 3 võrdseks osaks),
  • kolmnurga 135 saamiseks joonestame kaare ringjoone ülemisest telgpunktist vertikaalteljel raadiusega R80; kaare ja ringjoone lõikepunktid määravad punktid 1 ja 3.

C. Võtame kahe järjestikuse jaotuspunkti vahemiku (kõõlu) sirklisse ja kontrollime sellega üle, kas kõik kõõllõikude pikkused (jaotuspunktide vahekaugused) on võrdsed. Ühendame jaotuspunktid järjestikku kõõludega.

Korrastame joonise ja vormistame tekkinud korrapärase kõõlhulknurga pideva laijoonega.
Näide 4.2. Korrapärane kõõlkuusnurk kahe korrapärase kõõlkolmnurga konstrueerimisega; kolmnurkade tipud asuvad ringjoone telgpunktides horisontaalteljel 
Ringjoone jaotamiseks kasutame sirklit ja joonlauda.

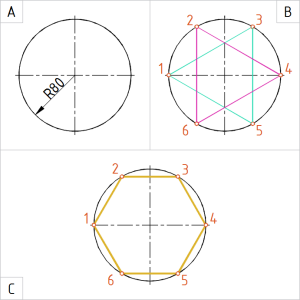Joonis. Ringjoone 6 võrdseks osaks jaotamisel asuvad kahe korrapärase kõõlkolmnurga tipud 1 ja 4 ringjoone telgpunktides horisontaalteljel

 A. Joonestame ringjoone raadiusega 80 mm.
B. Jaotame ringjoone kaks korda kolmeks:

  • kolmnurga 135 saamiseks joonestame kaare ringjoone parempoolsest telgpunktist horisontaalteljel raadiusega R80; kaare lõikepunktid ringjoonega määravad punktid 3 ja 5,
  • kolmnurga 246 saamiseks joonestame kaare ringjoone vasakpoolsest telgpunktist horisontaalteljel raadiusega R80; kaare lõikepunktid ringjoonega määravad punktid 2 ja 6.

C. Võtame sirklisse ringjoone kahe järjestikuse jaotuspunkti vahemiku (kõõlu) ja kontrollime üle, kas kõik kõõlud võrdsed. Ühendame jaotuspunktid järjestikku kõõludega.

Korrastame joonise ja vormistame tekkinud korrapärase kõõlhulknurga pideva laijoonega.
(3) Iseseisev harjutus:

Joonesta ringjoon (R > 29 mm) ja selle sisse korrapärane kõõlkuusnurk nii, et kuusnurga tippude paar asub ringjoonel telgjoontest tekkinud nurga poolitajal.
Näide 4.3. Ringjoonele korrapärase kõõlkuusnurga tippude tuletamine, kasutades kesknurga abi
Ringjoone jaotamiseks kasutame kahte joonlauda. Neist üks peab olema täisnurkne kolmnurk teravnurkadega 30° ja 60°.

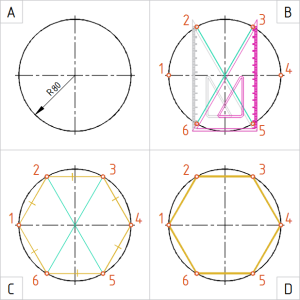Joonis. Ringjoone jaotamine 6 võrdseks osaks kasutades teravnurkadega 30° ja 60° täisnurkset kolmnurkjoonlauda

 Ringjoon tekib 360-kraadise täispöördega. Kui jaotame 360 kraadi kuueks võrdseks osaks (360/6), saame korrapärase hulknurga kesknurgaks (s.o kahe raadius-joone vaheliseks nurgaks) 60 kraadi. Nüüd on võimalus kasutada ringjoone kuueks jaotamisel töövahendina 30- ja 60-kraadiste teravnurkadega täisnurkset kolmnurka.

A. Joonestame ringjoone raadiusega 80 mm.

B. Kasutame paralleellüket. Antud näitel asuvad kuusnurga tipud 1 ja 4 ringjoone telgpunktides horisontaalteljel. Ülejäänud punktid tuletame paari kaupa paralleellükkega.

  • Kolmnurkjoonlaua lühem kaatetserv ja hüpotenuusserv moodustavad 60-kraadise nurga. Joondame kolmnurkjoonlaua pikema kaatetserva paralleelseks vertikaalteljega. Lühem kaatetserv on all ja joonlaua täisnurkne nurk asub vasakul. Asetame lühema kaatetserva alla tugijoonlaua (vt rist- ja paralleelsirgete joonestamine) ja hoiame seda vasaku käe sõrmedega kindlalt paigal. Parema käega nihutame kolmnurka vertikaalteljest vasakule, kuni hüpotenuusserv läbib ringjoone keskpunkti. Täpselt läbi ringjoone keskpunkti joonestame ringjoonele diameetri – sirge, mis märgib ringjoonega lõikumisel jaotuspunktid 2 ja 5.
  • Pöörame kolmnurkjoonlaua tugijoonlaual ümber. (Joondame täisnurkse kolmnurga pikema kaatetserva paralleelseks vertikaalteljega. Lühem kaatetserv on all ja  kolmnurga täisnurkne nurk paremal. Lühema kaatetserva all on tugijoonlaud, mida hoiame vasaku käe sõrmedega kindlalt paigal.) Parema käega nihutame kolmnurka paremale, kuni hüpotenuusserv läbib ringjoone keskpunkti. Täpselt läbi ringjoone keskpunkti joonestame diameetri – sirge, mis määrab ringjoonel jaotuspunktid 3 ja 6.

C. Võtame sirklisse kahe järjestikuse jaotuspunkti vahemiku (kõõlu) sirklisse ja kontrollime üle, kas kõik jaotuspunktide vahekaugused on võrdsed. Ühendame jaotuspunktid järjestikku kõõludega.

D. Korrastame joonise. Vormistame tekkinud korrapärase kõõlhulknurga pideva laijoonega.

(5) Ringjoone jaotamine seitsmeks võrdseks osaks

Kasutame sirklit ja joonlauda.

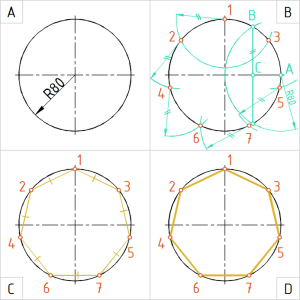Joonis. Ringjoone jaotamine 7 võrdseks osaks

 A. Joonestame ringjoone raadiusega 80 mm.
B. Poolitame raadiuslõigu horisontaalteljel ringjoone keskpunktist paremal.
Selleks joonestame punktist A kaare ringi raadiusega 40 mm (läbib täpselt ringi keskpunkti). Ringjoone ja kaare lõikepunktide ühendamisel joonestame raadiuslõigu keskristsirge – see poolitab raadiuslõigu punktis C. Võtame sirklisse lõigu BC  ja ringjoone ülemisest telgpunktist alustades märgime ringjoonele lõigu BC pikkusega joonestatud kaartega ülejäänud jaotuspunktide asukohad.
C. Kontrollime üle, kas kõik jaotuspunktide vahekaugused on võrdsed. Ühendame jaotuspunktid järjestikku kõõludega.
D. Korrastame joonise. Vormistame tekkinud korrapärase kõõlhulknurga pideva laijoonega.

(6) Ringjoone jaotamine kaheksaks võrdseks osaks

Kasutame sirklit ja joonlauda.

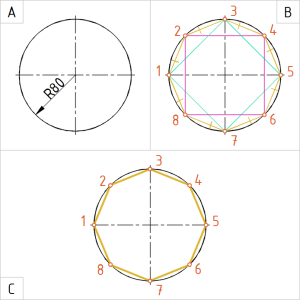Joonis. Ringjoone jaotamine 8 võrdseks osaks

 A. Joonestame ringjoone raadiusega 80 mm.
B. Konstrueerime ringjoone sisse kaks nelinurka:

  • esimese nelinurga tippudeks 1, 3, 5  ja 7 on ringjoone telgpunktid,
  • teise nelinurga tipud 2, 4, 6  ja 8 saame, kui poolitame telgjoonte lõikumisel moodustunud täisnurgad (vt ringjoone jaotamine 4 võrdseks osaks).

C. Vormistame joonise:

  • ühendame jaotuspunktid ringjoonel järjestikku kõõludega,
  • kontrollime üle, et kõik kõõllõigud on ühepikkused,
  • korrastame joonise ja joonestame kõõlud pideva laijoonega.

(7) Ringjoone jaotamine kümneks võrdseks osaks

Kasutame sirklit ja joonlauda.

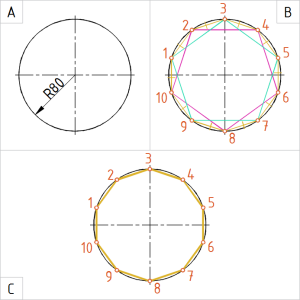Joonis. Ringjoone jaotamine 10 võrdseks osaks

 A. Joonestame ringjoone raadiusega 80 mm.
B. Jaotame ringjoone kaks korda viieks võrdseks osaks, näiteks:

  • esimese viisnurga (13579) üks tippudest (3 ) asub ringjoone vertikaalteljel ülemises telgpunktis (vt ringjoone jaotamine 5 võrdseks osaks),
  • teise viisnurga (246810) üks tippudest (8 ) asub ringjoone vertikaalteljel alumises telgpunktis.

C. Vormistame joonise:

  • tuletatud hulknurga tipud ühendame järjestikku kõõludega,
  • kontrollime, et kõik kõõlud on ühepikkused,
  • korrastame joonise ja joonestame kõõlud üle pideva laijoonega.

(8) Ringjoone jaotamine kaheteistkümneks võrdseks osaks

Kasutame sirklit ja joonlauda.

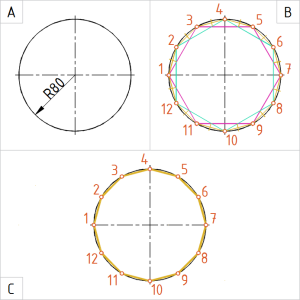Joonis. Ringjoone jaotamine 12 võrdseks osaks

 A. Joonestame ringjoone raadiusega 80 mm.
B. Jaotame ringjoone kas:

  • kaks korda kuueks võrdseks osaks või
  • neli korda kolmeks võrdseks osaks

(Vt eelnevalt kirjeldatud jaotamist 3- või 6-ks.) Kontrollime lahendust.

C. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.

(9) Ringjoone jaotamine neljateistkümneks võrdseks osaks

Kasutame sirklit ja joonlauda.

Joonis. Ringjoone jaotamine 14 võrdseks osaks

 A. Joonestame ringjoone raadiusega 80 mm.
B. Jaotame ringjoone kaks korda seitsmeks võrdseks osaks. (Vt ringjoone jaotamine 7-ks.) Kontrollime lahendust.
C. Korrastame joonise ja joonestame kõõlud üle pideva laijoonega.

Vaata lisaks

[1] Joonestamine. Õpilase raamat (Tehnotiiger)