Nurk. Konstruktsioonid sirkli ja joonlauaga

Nurkade konstrueerimine sirkli ja joonlauaga ning arvutis on joonestustöös sage ülesanne. Joonist tehes kulub marjaks ära teadmine, mis on nurk, ja oskus joonestada eri suuruses nurki.

Manuaalsel nurga konstrueerimisel ja jaotamisel võime kasutada:

malli ja joonlauda,
sirklit ja joonlauda.

Mall ja joonlaud

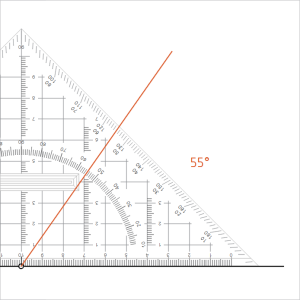Joonis. Nurga suuruse mõõtmine malli abil

Malli kasutamisel:

asetame malli antud sirgjoonele ning (sätime kohakuti sirgjoonel märgitud punkti s.o nurga tipp) ja malli 0-punktiga,
märgime skaalalt lühikese märkejoonega nurga soovitud suuruse; tõstame malli eemale,
ühendame nurga tipu ja märkejoone sirgega.

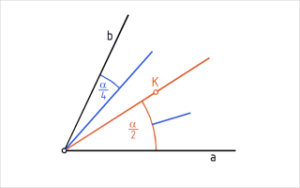
Kiir, mis pöörab end tasandil ühe punkti ümber (nurga tipp), tekitab oma algasendi suhtes nurga. Nurk on tasandiosa pöörleva kiire alg- ja lõppasendi vahel. Nurka piiravaid kiiri nimetame nurga haaradeks.

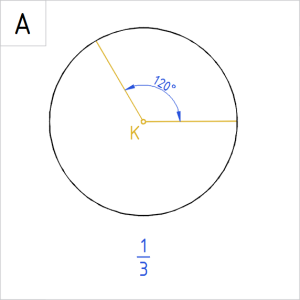
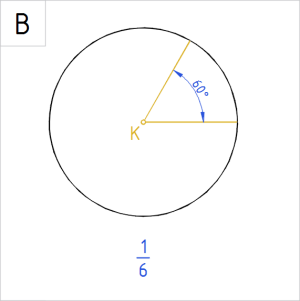
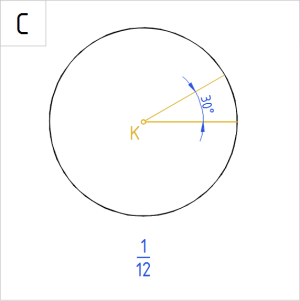
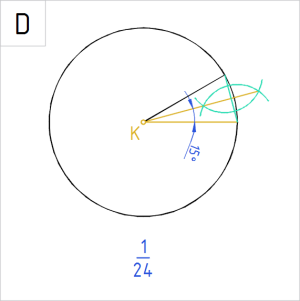
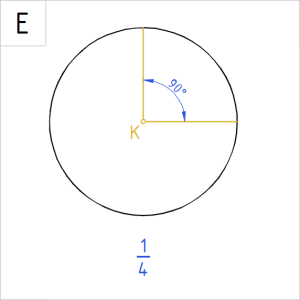
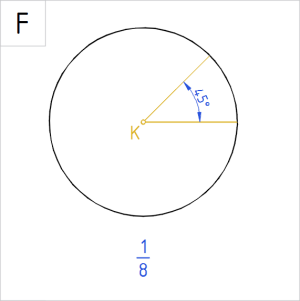
Allpool on ringidele märgitud valik nurkade suurusi kraadides. Ringjoone alla on kirjutatud, kui suure osa nurk ringist (või ringjoonest) kui tervikust eraldab.

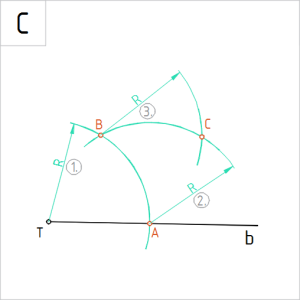
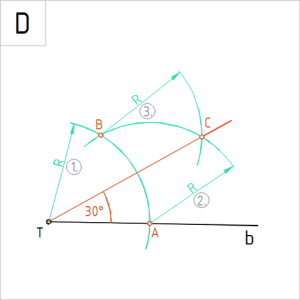
Antud nurga poolitamisel, nagu näitavad joonised C ja D, märgib poolnurk antud nurgast kaks korda väiksemat osa.

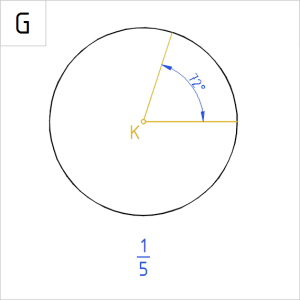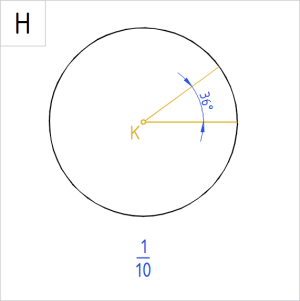Joonis. Ringi sektorid

Loe lisaks ringjoone jaotamine võrdseteks osadeks sirkli ja joonlaua abil.

Sirkel ja joonlaud

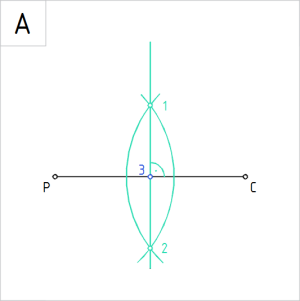
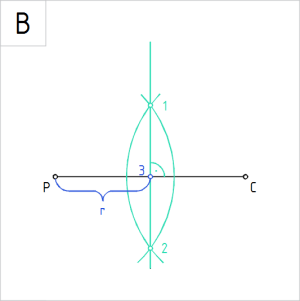
Nurga poolitamine sirkli ja joonlaua abil

Nurga võrdseteks osadeks jaotamisel sirkli ja joonlaua abil saame nurka jaotada vaid paarisarvuks jaotisteks.

Konstruktsioon põhineb nurga poolitamisel. Kui eesmärk on jaotada nurk näiteks neljaks, siis esmalt poolitame antud nurga. Seejärel poolitame mõlemad poolnurgad.

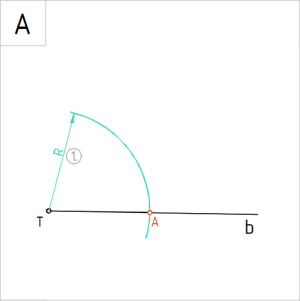
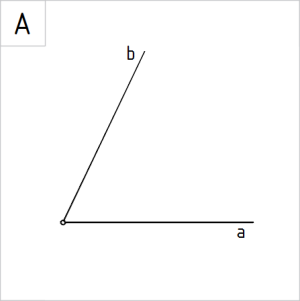Joonis. Nurk (a, b)	Ülesanne 1. Joonestada vabalt valitud suurusega teravnurk (a, b). Poolitada nurk ∠ (a, b).
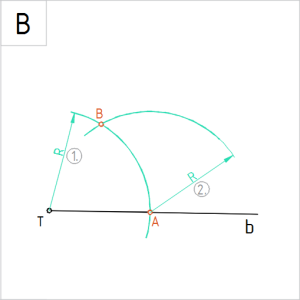
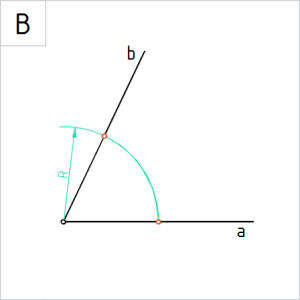Joonis. Kaar vabalt valitud raadiusega R	B. Joonestame kaare vabalt valitud raadiusega R lõikuma nurga haaradega a ja b.
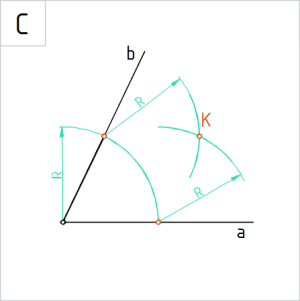Joonis. Nurga poolitajat määrav punkt K	C. Tuletame teise nurga poolitajat määrava punkti K. Selleks joonestame kaare R lõikepunktidest haaradel a ja b uued kaared raadiusega R. Nurga tipp on nurka poolitava sirge üks punkt ning kaarte lõikepunkt K on seda sirget määrav teine punkt.
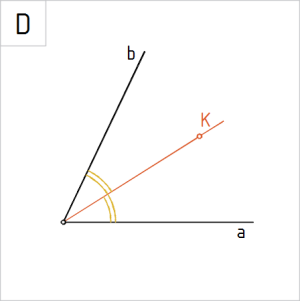Joonis. Nurga poolitaja läbi punkti K	D. Joonestame nurga tipust läbi punkti K nurga poolitaja kitsa pidevjoonega.

30° nurga konstrueerimine sirkli ja joonlaua abil

Joonis. Konstruktsioon raadiusega R joonestatud kaar määrab sirgel b punkti A	Ülesanne 2. Antud sirge b on nurga üks haar. Konstrueerida sirkli ja joonlaua abil punktist T 30° nurk. A. Joonestame punktist T vabalt valitud raadiusega R kaare, mille lõikepunkt määrab sirgel b punkti A.
Joonis. Sama raadiusega R joonestatud kaar punktist A määrab konstruktsiooni punkti B	B. Joonestame punktist A sama raadiusega R kaare. Tähistame kaarte lõikepunkti punktiga B.
Joonis. Sama raadiusega R joonestatud kaar punktist B määrab nurga teise haara punkti C	C. Joonestame punktist B taas kord raadiusega R kaare. Kaarte lõikepunkti eelviimasena joonestatud kaarel tähistame punktiga C.
Joonis. ∠ CTA = 30°	D. Ühendades punktid T ja C, oleme joonestanud nurgale teise haara. Haaradevaheline nurk CTA on 30°.

45° nurga konstrueerimine sirkli ja joonlaua abil

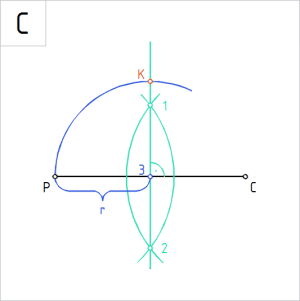
Joonis. Keskristsirge 12 poolitab lõigu PC punktis 3	Ülesanne 3. Antud sirglõik PC on nurga üks haar. Konstrueerida sirkli ja joonlaua abil punktist P 45° nurk. A. Poolitame antud lõigu PC keskristsirgega (12). Kasutame selleks kaart vabalt valitud raadiusega, mis vastab tingimusele R>\|PC\|/2. Tähistame sirglõigul PC keskristsirge lõikepunkti tähisega 3.
Joonis. Nurga teise haara määramiseks kasutame raadiuslõiku r = P3	B. Võtame sirklisse pool lõigu PC pikkusest – P3 ehk raadiuse r.
Joonis. Nurga teise haara määrab punkt K keskristsirgel	C. Joonestame punktist 3 raadiusega P3 kaare lõikuma keskristsirgega. Tähistame kaare ja ristsirge joonte lõikepunkti tähisega K.
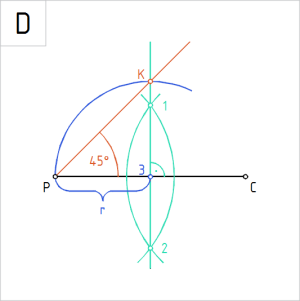Joonis. Teravnurk 45° on ∠ KPC	D. Ühendame punktid P ja K. Oleme joonestanud nurga teise haara. Nurk KPC on 45°.

60° nurga konstrueerimine sirkli ja joonlaua abil

Joonis. Punktist T vabalt valitud konstruktsioonlõiguga R joonestatud kaar määrab lõigul TM punkti 1	Ülesanne 4. Antud sirglõik TM on nurga üks haar. Konstrueerida sirkli ja joonlaua abil punktist T 60° nurk. A. Joonestame vabalt valitud pikkuses raadiuslõiguga R (R>\|TM\|/2) punktist T kaare. Kaare lõikepunkti antud sirglõigul TM tähistame punktiga 1.
Joonis. Punktist 1 sama konstruktsioonlõiguga R joonestatud vastukaar määrab nurga teisel haaral punkti K	B. Joonestame punktist 1 sama raadiuslõiguga R vastukaare. Kaarte lõikepunkti tähistame punktiga K. Punkt K kuulub nurga teisele haarale.
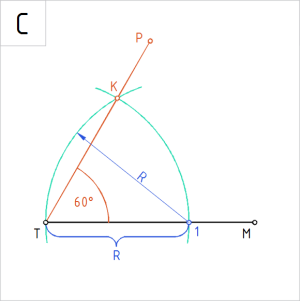Joonis. ∠ KTM = 60°	C. Ühendame punktid TK sirgega. Nurk KTM on 60°. (\|TM\| = \|TP\|, loe: lõigu TM pikkus võrdub lõigu TP pikkusega)

90° nurga konstrueerimine sirkli ja joonlaua abil

Kiire alguspunktist

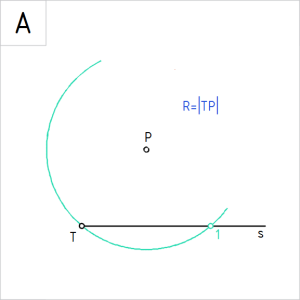Joonis. Punkti P suhtes sümmeetriliselt paiknevad konstruktsioonpunktid T ja 1 sirgel s	Ülesanne 5. Antud on sirge s ja punkt P, mis ei kuulu sirgele. Sirge s on nurga üks haar. Konstrueerida sirkli ja joonlaua abil sirgel s asuvast punktist T 90° nurk. A. Joonestame punktist P raadiuslõiguga TP kaare. Kaare lõikepunkti antud sirgel tähistame punktiga 1.
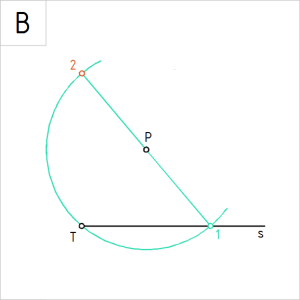Joonis. Täisnurga teine haar on määratud punktiga 2	B. Ühendame sirgega punktid 1 ja P ning pikendame selle sirge ringikaare diameetriks. Tähistame kaare ja sirge lõikepunkti tähisega 2. Punkt 2 kuulub nurga teisele haarale.
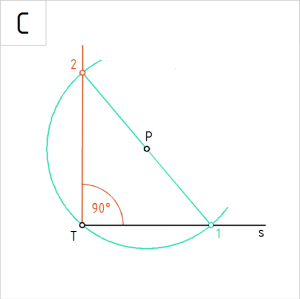Joonis. ∠ 2T1 = 90°	C. Ühendame punktid T2 sirgega kitsa pidevjoonega. Tuletatud nurk 2T1 on 90°.

Sirgel asuvast punktist

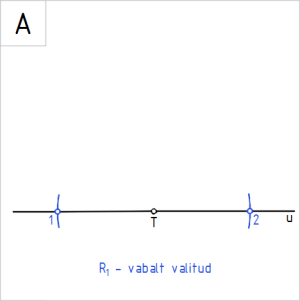Joonis. Sirgel u punkti T suhtes sümmeetriliselt paiknevate konstruktsioonpunktide märkimine	Ülesanne 6. Antud on sirge u ja sellel punkt T. Konstrueerida sirkli ja joonlaua abil punktist T 90° nurk. A. Joonestame vabalt valitud raadiuslõiguga R₁ punktist T kaare lõikuma sirgega u punkti T ümbruses ja tähistame sirgel kaare lõikepunktid 1 ja 2.
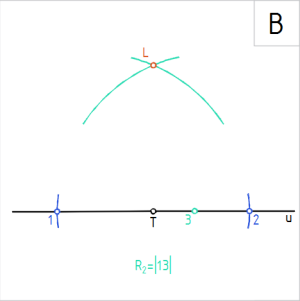Joonis. Antud sirgele u määravad ristsirge punktid T ja L	B. Võtame sirklisse vabalt valitud pikkusega raadiuslõigu R₂ (R₂>\|12\|/2, nt R₂ = \|13\|) ning joonestame sellega punkidest 1 ja 2 kaared. Tähistame kaarte lõikepunkti tähisega L. Punkt L kuulub nurga teisele haarale.
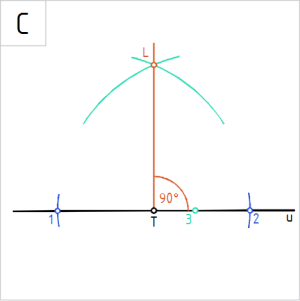Joonis. ∠ LT1 = 90° ja ∠ LT2 = 90°	C. Ühendame punktid TL sirgega. Tuletatud nurgad LT2 ja LT1 on 90°.

Kui vajame mingile antud sirglõigule ristsirget, mis läbib tema keskpunkti, siis tuletame antud sirglõigule keskristsirge ehk poolitame lõigu.

Sirgel mitteasuvast punktist

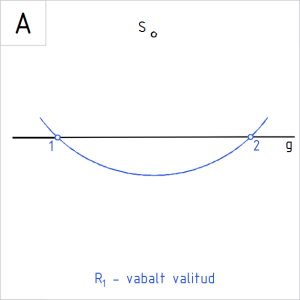Joonis. Konstruktsioonpunktide 1 ja 2 märkimine sirgele g	Ülesanne 7. Antud on sirge g ja punkt S, mis ei kuulu sirgele g. Konstrueerida sirkli ja joonlaua abil punktist S sirgele g ristsirge (90°). A. Kõigepealt valime antud sirgele mingi pikkusega lõigu. Selleks joonestame vabalt valitud raadiuslõiguga R₁, mis lõikub antud sirgega, punktist S kaare ja tähistame sirgel kaare lõikepunktid tähistega 1 ja 2.
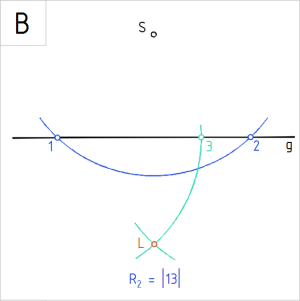Joonis. Ristsirget määrava punkti L tuletamine	B. Võtame sirklisse vabalt valitud pikkusega raadiuslõigu (R₂>\|12\|/2, nt R₂=\|13\|) ning joonestame sellega punkidest 1 ja 2 kaared punkti S suhtes teisele poole sirget g. Tähistame kaarte lõikepunkti tähisega L. Punkt L kuulub sirge g ristsirgele.
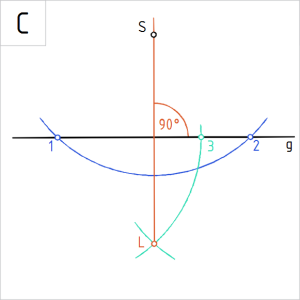Joonis. SL on risti sirgega g	C. Ühendame punktid SL sirgega kitsa pidevjoonega. Punktist S on joonestatud sirge g ristsirge SL (nurk 90°). Sirge g ristsirge määravad punktid SL.

Nurkade liitmine sirkli ja joonlaua abil

(1) Eelnevalt kirjeldatud konstruktsioonide baasil saame sirkli ja joonlauaga joonestada järgmiste suurustega nurki:

75° = 30° + 45°
105° = 45° + 60°
120° = 30° + 90° või 60° + 60°
135° = 90° + 45°
150° = 60° + 90°.

Siin konstrueerime järjestikku kaks nurka. Alustame ühe sirge joonestamisega. Selle külge konstrueerime nurga teise haara. Saadud haar on järgmisele nurgale esimene haar ehk antud sirge ning nüüd konstrueerime ka teisele nurgale teise haara.

(2) Vaatleme järgnevas kuidas liita teravnurkade suurusi sirkli ja joonlaua abil.

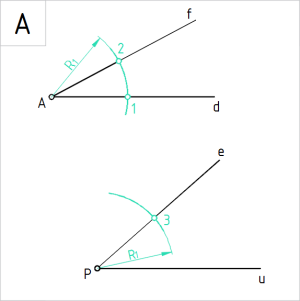
Joonis. Nurga konstruktsioonkaar lõikub väiksema nurga mõlema haaraga ja suurema nurga haaraga, mille külge liidame väiksema nurga	Ülesanne 8. Antud on nurgad ∠ (f, d) ja ∠ (e, u). Liida antud nurgad sirkli ja joonlaua abil. A. Liidame väiksema nurga suuremale. Joonestame vabalt valitud pikkuses raadiuslõiguga R₁ nurkade tippudest A ja P kaared ja tähistame nurga haaradel kaarte lõikepunktid: 1 ⊂ d, 2 ⊂ f ja 3 ⊂ e.
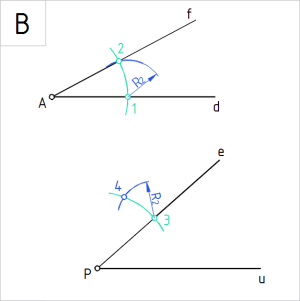Joonis. Kõõllõigu 12 pikkuse liitmine teisele nurgale	B. Võtame sirklisse raadiuslõigu R₂=\|12\| ning joonestame sellega kaare punktist 3. Tähistame kaarte lõikepunkti tähisega 4. Punkt 4 kuulub liidetud nurga teisele haarale.
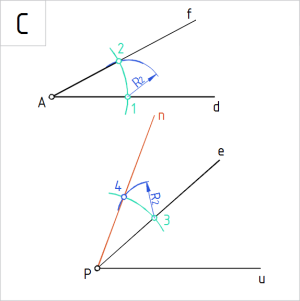Joonis. Kahe antud nurga summa on ∠ (n, u)	C. Ühendame punktid P4 sirgega n. Liidetud nurk ∠ (e, n) on suuruselt võrdne nurgaga ∠ (f, d). Kahe nurga summa on ∠ (n, u).

Nurga koopiakujund sirkli ja joonlaua abil

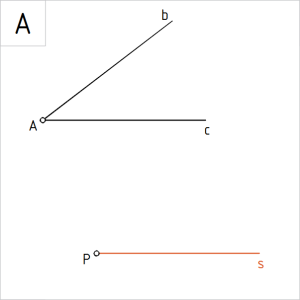Joonis. Ülesande 8 algandmed	Ülesanne 9. Antud on sirge s ja punkt P, mis kuulub sirgele s ning nurk (c, b). Konstrueerida sirkli ja joonlaua abil punktist P sirgele s samasuguse suurusega nurk, nagu on ∠ (c, b ).
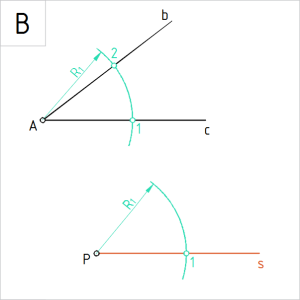Joonis. Nurga haaradel on konstruktsioonpunktid	B. Joonestame vabalt valitud raadiuslõiguga R₁ punktidest A ja P kaared ja tähistame kaarte lõikepunktid horisontaalsetel sirgetel tähisega 1 ja kaldsirgel tähisega 2.
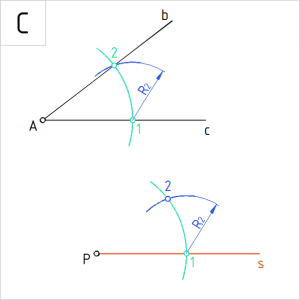Joonis. Kõõllõigu 12 pikkuse üle kandmine	C. Võtame sirklisse kõõllõigu R₂ = \|12\| ning joonestame sellega kaare sirge s punktist 1. Tähistame kaarte lõikepunkti tähisega 2. Punkt 2 kuulub konstrueeritava nurga teisele haarale r .
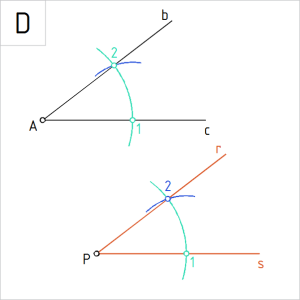Joonis. ∠ 1P2 = ∠ 1A2	D. Ühendame punktid P2 sirgega. Tuletatud ∠ 1P2 = ∠ 1A2 .