Nurk
Nurk tekib, kui kiir pöörab end tasandil ühe punkti ümber. Nurk määrab, millise „tüki“ kiir tasandist eraldab.
Mõned nurgaga seotud mõisted:
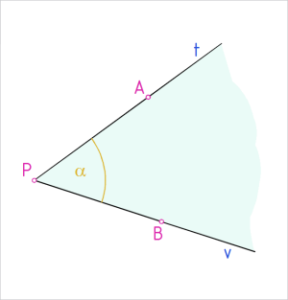 Joonis 1. Nurk |
Pöörde keskpunkti nimetatakse nurga tipuks (P ).
Tasandiosa piiravaid kiiri nimetatakse nurga haaradeks (t ja v). Pöörleva kiire alg- ja lõppasendi vahelist tasandiosa nimetatakse nurgaks. Nurka tähistame kasutades kas:
|
Nurga suuruse mõõtmisel võrdleme nurka täispöördega ning kirjeldamisel kasutame kraadimõõtu.
Kraadimõõt sisaldab:
- nurgakraadi (1°); saame jaotades täispöörde 360° võrdseks osaks,
- nurgaminutit (1′); saame jaotades nurgakraadi 60 võrdseks osaks,
- nurgasekundit (1″); saame jaotades nurgaminuti 60 võrdseks osaks.
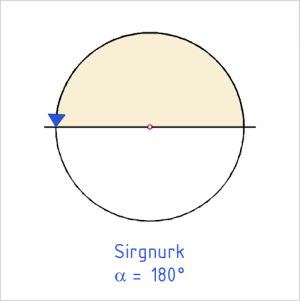
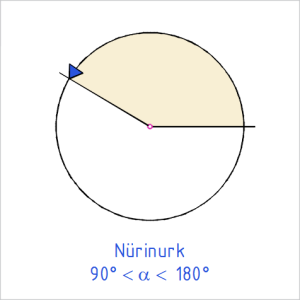
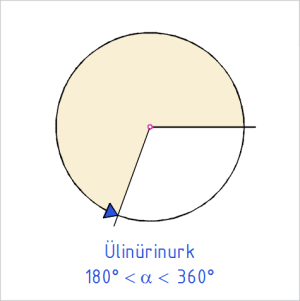
Nurkade liigid
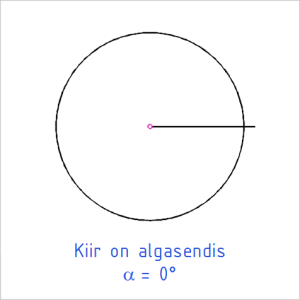 |
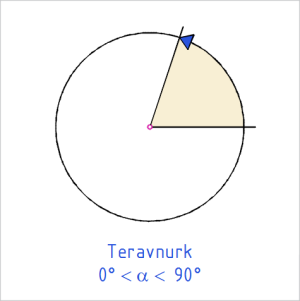 |
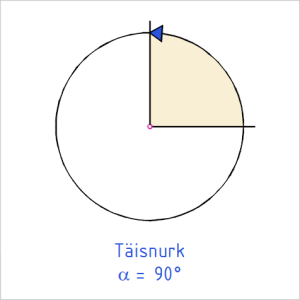 |
 |
 |
 |
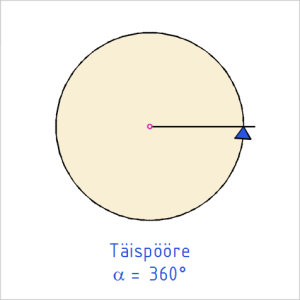 |
Tabel 1. Nurkade liigid
Orienteeritud nurk
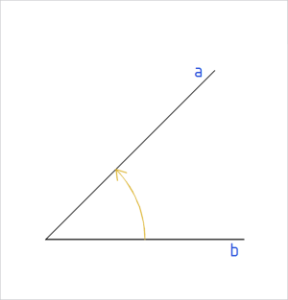 Joonis 2. Positiivne nurk: ∠ (b, a) |
Arvutigraafikas kasutame nurga suuruse kõrval ka mõistet orienteeritud nurk. See tähistab kiire pöörlemise suunda.
Tavaliselt pöörleb kiir tasandil vastu kellaosuti liikumise suunda. Nurka, mis tekib kiire pöörlemisel vastu kellaosuti liikumise suunda, nimetame vasaksuunalise orientatsiooniga nurgaks ehk positiivseks nurgaks (joonis 2). Näiteks nurga suuruse märgime arvuna 45° (ehk +45°). See tähendab, et nurk on saadud kiire matemaatiliselt positiivsel pöörlemisel. |
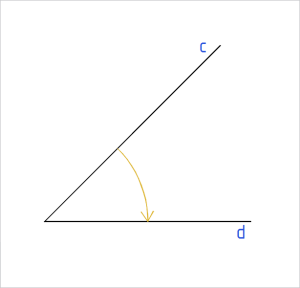 Joonis 3. Negatiivne nurk: ∠ (c, d) |
Nurka, mis tekib kiire pöörlemisel kellaosuti liikumise suunas, nimetame paremsuunalise orientatsiooniga nurgaks ehk negatiivseks nurgaks (joonis 3).
Näiteks nurga suuruse märgime arvuna -45°. See tähendab, et nurk on saadud kiire matemaatiliselt negatiivsel pöörlemisel. |
Nurga joonestamine
Malliga
Nurga suurust mõõdame malliga. Positiivset nurka märgime vastu kellaosuti liikumise suunda ning alustame kiire algasendist (0°), mille suund on alguspunktist O horisontaalselt vasakul.
Näiteks joonestame malli abil nurgad 30°, 38° ja 155°:
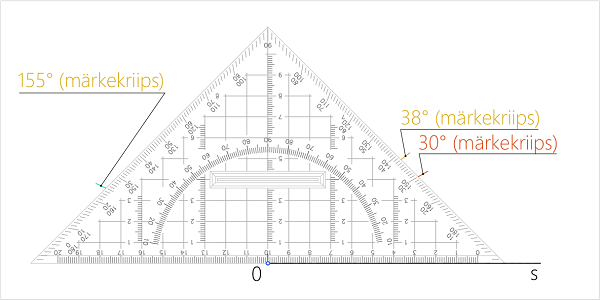 Joonis 4. Mallilt 30°, 38° ja 155° nurga märkimine (1) Sirge s on nurkadele 30°, 38° ja 155° üheks haaraks. Nurga teise haara asukoha mõõdame mallilt. Selleks joondame malli alusserva sirgele s, asetades malli 0-punkti nurga tippu O. Loeme malli skaalalt vastupäeva liikudes vajalikud kraadimõõdud, märgistades nende asukohad lühikeste märkekriipsudega. |
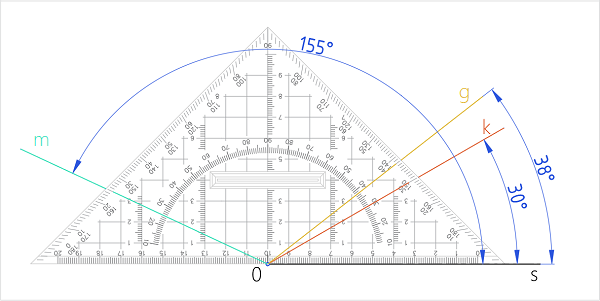 Joonis 4. Mallilt 30°, 38° ja 155° nurgale teise haara joonestamine (2) Sirgel s asuva nurga tipust O joonestame nurkadele läbi vastavate nurkade märkekriipsude teise haara. |
Sirkli ja joonlauaga
Arvutil
Arvutis nurga joonestamiseks on oluline teada orienteeritud nurga olemust.
Vaata lisaks
[1] Vikipeedia (nurk)