Korrapärane hulknurk
Korrapärane hulknurk leiab joonestamisel palju kasutamist. See on mitmesuguste hulktahkude põhjadeks ja/või tahkudeks.
Korrapärasel n-nurgal on n võrdset külge ja n võrdset nurka.
Korrapärane hulknurk on sümmeetriline.
Korrapärase hulknurga tippude arvu suurendamisel läheneb ta üha enam ringjoonele.
Määrav kolmnurk
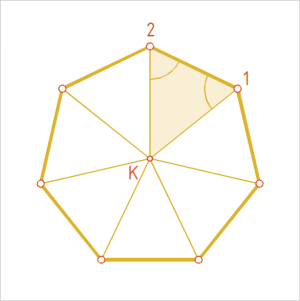 Joonis 1. Määrav kolmnurk 1K2 |
Korrapärane hulknurk koosneb n võrdsest võrdhaarsest (joonis 1; ∆ 1K2) kolmnurgast, nn määravast kolmnurgast.
Erijuhul on korrapärase hulknurga määrav kolmnurk võrdkülgne (joonis 4). |
Sise- ja ümberringjoon
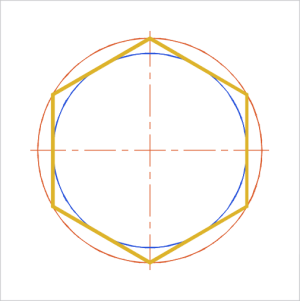 Joonis 2. Korrapärase hulknurga sise- ja ümberringjoon |
Igal korrapärasel n-nurksel hulknurgal on sise- ja ümberringjoon (joonis 2). |
Siseringjoon
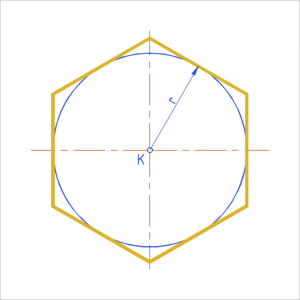 Joonis 3. Korrapärase hulknurga siseringjoon |
Siseringjoon puudutab hulknurga külgi. Määrava kolmnurga alusele tõmmatud kõrgus on siseringjoone raadius r. |
Ümberringjoon
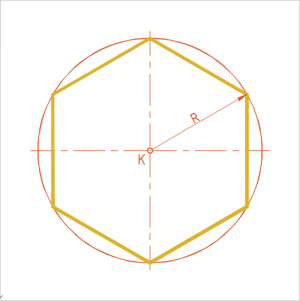 Joonis 4. Korrapärase hulknurga ümberringjoon |
Ümberringjoon läbib hulknurga tippe. Määrava kolmnurga haar on ümberringjoone raadius R.Teame, et kõõl on joone kahte punkti ühendav lõik, mis ei lõiku selle joonega. Ümberringjoone punkte ühendavad kõõlud on võrdsete pikkustega ning võime hulknurka nimetada ka korrapäraseks kõõlhulknurgaks. |
Ringjoonele lähenev korrapärane hulknurk
 Joonis 5. 20-nurkne korrapärane hulknurk koosneb 20 võrdhaarsest kolmnurgast |
|
Kumer ja tähthulknurk
| Korrapärased hulknurgad võivad olla kas kumerad või tähekujulised.
Kumer tasandiline hulknurk jääb igast oma küljest või selle pikendusest ühele poole. Ükski kumera hulknurga sisenurk ei ole suurem kui 180°. Korrapärast tähthulknurka tähistame Schläfli sümboliga {p/q}, kus p on tippude arv ja q on (tippude) tihedus. Need on algarvud ning q ≥ 2. Hulknurga tiheduse võime nimetada ka tema pöördenumbriks. 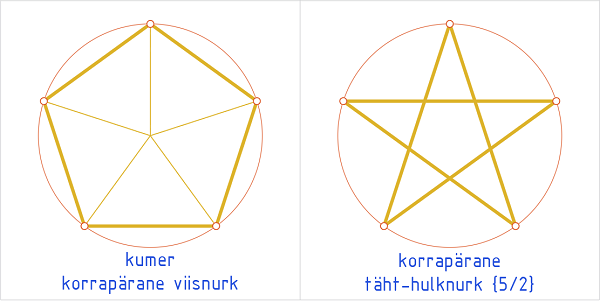 Joonis. Korrapärane kumer ja tähtviisnurk 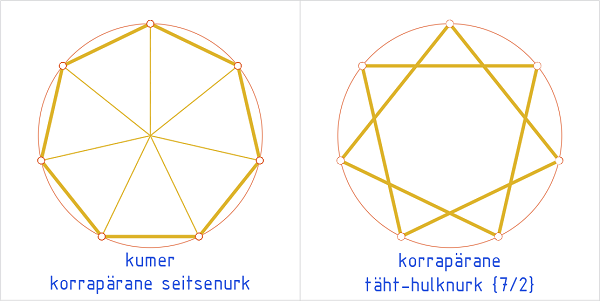 Joonis. Korrapärane kumer ja tähtseitsenurk |