Sirglõigu jaotamine võrdseteks osadeks

Sirglõigu jaotamine võrdseteks osadeks on geomeetria põhikonstruktsioon. Järgnevalt kirjeldame töövõtteid, mida manuaalsel joonestamisel sageli vaja läheb. Esmalt tuletame meelde terminid ja kirjaviisid.

Sirge, kiir ja lõik on mõisted, mille tähenduse teadmine võib probleemülesannete lahendamisel olla võtmetähtsusega:

Sirgel pole ei algus- ega lõpp-punkti. Tähistame sirget kas sellel asuva punktipaari tähistega, näiteks AB, või üldkujul ühe väiketähega, näiteks a. AB = a.
Kiirel ehk poolsirgel on alguspunkt, aga ei ole lõpp-punkti. Tähistame kiirt punktipaari tähistega, näiteks AB, kus punkt A on kiire alguspunkt, teist nimega punkti B läbib sirge kujutis, kuid see ei ole lõpp-punkt.
Lõigul on nii algus- kui lõpp-punkt. Tähistame lõiku selle otspunktide tähistega, näiteks AB.

Osadeks jaotame vaid lõiku. Sirgel ja kiirel saame valida või märkida punktid, mis lõigu määravad.

Mis erinevus on kirjapiltidel AB ja |AB|?

Sirglõik AB all mõistame sirge AB punkte, mis asetsevad A ja B vahel ning kus punktid A ja B on selle lõigu otspunktid.

Pikkus |AB | all mõistame lõigu AB suurust, mis näitab, kui mitu korda mahub pikkusühik lõigule AB.

Sirglõiku saame võrdseteks osadeks jaotada:

joonlaua mõõtskaala abil, kui sirglõigu pikkus jagub jaotiste arvuga täpselt,
abisirge ja vaba pikkusega ühiklõigu abil, kui sirglõigu pikkus kas jagub või ei jagu jaotiste arvuga täpselt (jagatis ei ole täisarv; nt on jagatis 8,13),
sirkli ja joonlaua abil, kui soovime lõiku poolitada. (Sama konstruktsiooni saame lõigule paarisarv-jaotiste tekitamiseks kasutada korduvalt.)

Tähelepanu! Punkti täpne asukoht on punktkujutise tähistamiseks kasutatud ringikese keskpunkt.

(1) Sirglõigu poolitamine

Lahendamisel kasutame sirklit ja joonlauda.
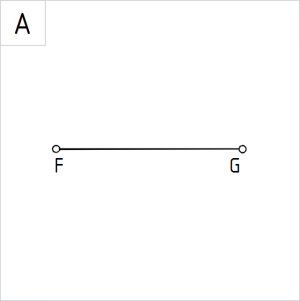Joonis 1.A. Sirglõik FG	Ülesanne 1. Poolitada lõik FG. (Joonis 1.A)
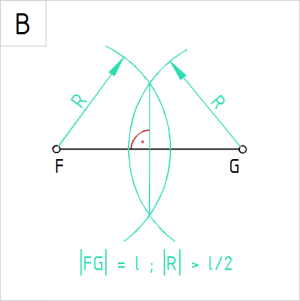Joonis 1.B. Sirglõigu FG keskristsirge	B. Konstrueerime sirglõigule FG keskristsirge, mis poolitab antud sirglõigu. Selleks joonestame sirglõigu otspunktidest F ja G sama raadiusega R kaared. Kaare raadiuse R valime vabalt, kuid tingimusega, et see on suurem kui l÷2, kus l on sirglõigu pikkus. Kaarte lõikepunktid ühendame sirgega. Oleme joonestanud lõigu FG keskristsirge. Kontroll: (1) Parim viis keskristsirge väljajoonestamiseks ja ühtlasi lahenduse kontrollimiseks, on joonestada lõigule läbi tuletatud kaarte lõikepunktide joonlaudade abil ristsirge. (2) Võtame lõigul FG sirklisse vahemiku lõigu ühest otspunktist kuni keskristsirge lõikepunktini, hoiame sirkli teravikku lõigu keskpunktis paigal ja pöörame sirkli teise haara lõigu teise otspunkti. Vastus on täpne, kui pööratud haara teravik maabub lõigu teises otspunktis.
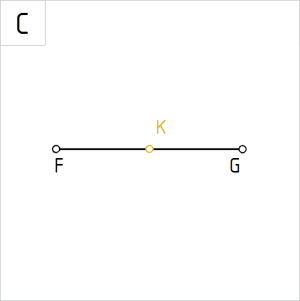Joonis 1.C. Punkt K poolitab sirglõigu FG	C. Tähistame keskristsirge lõikumiskoha punktkujutise ja tähisega. Korrastame joonise. Sirglõigu FG poolitab punkt K.

(2) Sirglõigu jaotamine osadeks

Näide 2.1. Lõigu pikkus jagub jaotiste arvuga täpselt. Jaotiste märkimisel kasutame joonlauda.
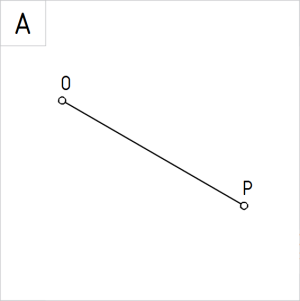Joonis 2.1. Sirglõik OP	Ülesanne 2.1. Jaotada lõik OP kümneks võrdseks osaks.
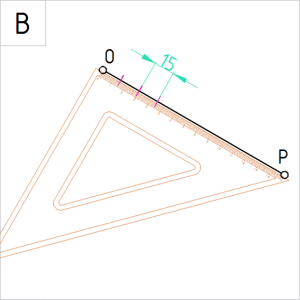Joonis 2.1.B. Sirglõigule OP jaotiste mõõtmine ja märkimine	B. \|OP \| = 150 mm (loe: lõigu OP pikkus võrdub 150 mm). Pärast jagamistehet 150÷10 saame ühe jaotise pikkuseks 15 mm. Asetame joonlaua mõõtskaalaga serva vastu sirglõiku OP paralleelselt ning mõõtskaala 0-punkti lõigu otspunkti O. Märgime lõigule lühikeste kriipsudega jaotiste pikkused.
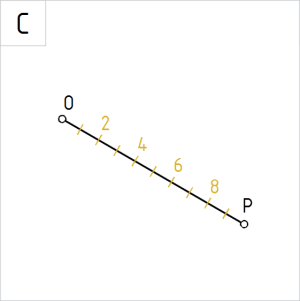Joonis 2.1.C. Sirglõigul OP on 10 võrdse pikkusega osa	C. Korrastame joonise. Sirglõik OP on jaotatud 10 võrdseks osaks. Kontroll: võtame (mõõt)sirklisse vahemiku O1, jättes sirkli haara punktis 1 paigale, pöörame sirkli teise haara punkti 2 ning hindame märgitud lõikude võrdsust. Jätkame ülejäänud lõikude kontrollimist sirkli ühe haara paigalhoidmise ja teise haara pööramisega.
Näide 2.2. Lõigu pikkus ei jagu jaotiste arvuga täpselt. Lahendamisel kasutame vaba sihiga sirge ja vabalt valitud ühiklõigu abi. Lahendamisel kasutame joonlaudu või joonlauda ja sirklit.
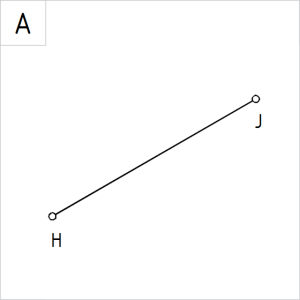Joonis 2.2. Sirglõik HJ	Ülesanne 2.2. Jaotada sirglõik HJ seitsmeks võrdseks osaks.
Joonis 2.2.B. Abisirge q ja ühiklõigud pikkusega a	B. (1) Joonestame sirglõigu ühest otspunktist (nt H) vaba sihiga sirge q. (2) Märgime sirgel q vabalt valitud ühiklõigu pikkusega a (nt 10 mm) nõutud arv (7) võrdset jaotist väikeste kriipsudega.
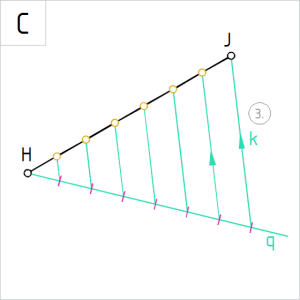Joonis 2.2.C. Kiir k ja temaga paralleelsete kiirtega jaotuspunkide üle kandmine sirglõigule HJ	C. Ühendame sirgel q seitsmenda jaotispunkti antud lõigu teise otspunktiga J. Nimetame ühendusjoone kiireks k. Kannamesirglõigule HJ kiirega k paralleelselt üle kõik sirgel q märgitud jaotuspunktid . Parim viis seda teha on paralleellükke abil. (Nooled näitavad joone tõmbamise suunda, nt joonis 2.2.C jt.) Kontroll: võtame (mõõt)sirklisse esimese vahemiku alates punktist H, jätame sirkli haara esimeses jaotuspunktis paigale, pöörame sirkli teise haara teise jaotuspunkti ning hindame märgitud lõikude võrdsust. Jätkame ülejäänud lõikude kontrollimist sirkli ühe haara paigalhoidmise ja teise haara pööramisega.
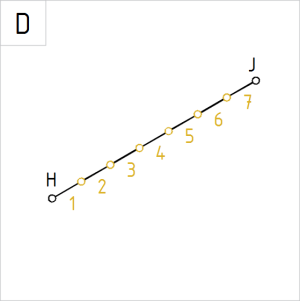Joonis 2.2.D. Sirglõigul HJ on 7 võrdse pikkusega osa	D. Korrastame joonise. Sirglõik HJ on jaotatud 7 võrdseks osaks.

(3) Sirglõigu jaotamine suhtes

Lõigu jaotamisel kasutame kahte joonlauda, millest vähemalt üks on täisnurkne kolmnurk.
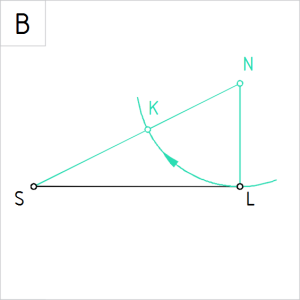
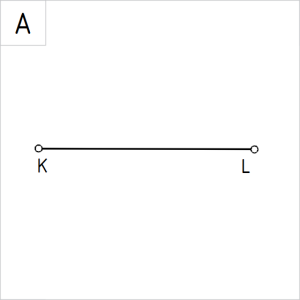Joonis 3. Sirglõik KL	Ülesanne 3. Tuletada lõigul KL punkt M nii, et kehtiks tingimus KM÷ML = 2÷3.
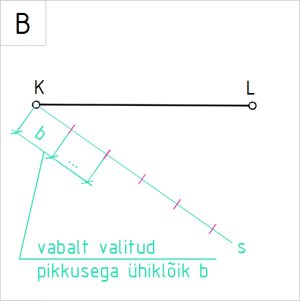Joonis 3.B. Vaba sihiga sirge s ja ühiklõik b	B. Tingimus KM÷ML = 2÷3 ütleb, et sirge pikkusest moodustab lõik \|KM\| 2 osa ja lõik \|ML\| 3 osa. Seega peame sirgele KL märkima 2 + 3 = 5 osa. Selleks joonestame sirglõigu KL ühest otspunktist vaba sihiga sirge s. Märgime sirgel s vabalt valitud ühiklõiguga b (nt 12 mm) 5 osa ehk 5 võrdse pikkusega jaotist.
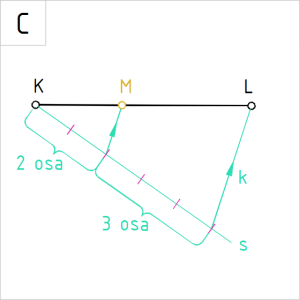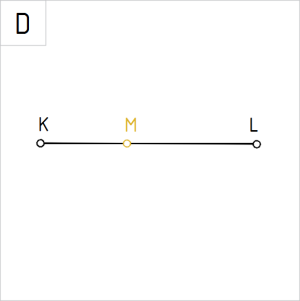Joonis 3.C. Kiir k ja punkti M asukoha üle kandmine sirglõigule KL	C. Ühendame sirgel s viienda jaotuspunkti antud lõigu teise otspunktiga L. Nimetame ühendusjoone kiireks k. Loendame abisirgel s alates punktist K kaks jaotist ja kanname kiire k paralleelsirgega punkti M asukoha üle sirgele KL. Kontroll: võtame (mõõt)sirklisse vahemiku KM (kontrolllõik), jätame sirkli haara jaotuspunktis M paigale, pöörame sirkli teise haara teise jaotuspunkti poole, asetame selle sirglõigule ning pöörame sirklit veel korra. Viimasel pööramisel peab punkt L jääma täpselt kontrolllõigu keskele.
Joonis 3.D. KM : ML = 2 : 3	D. Korrastame joonise. Punkt M jaotab sirglõigu KL suhtes KM÷ML = 2÷3.

(4) Sirglõigu jaotamine kuldlõikes

Lahendamisel kasutame sirklit ja joonlauda.
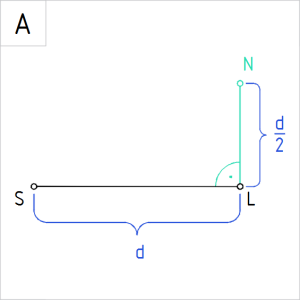Joonis 4.A. Sirglõigu SL ristlõik LN	Ülesanne 4. Jaotada lõik SL kuldlõikes. A. Joonestame lõigu SL (\|SL\| = d) ühest otspunktist, näiteks punktist L, lõigule esialgu vaba pikkusega ristsirge. Mõõdame ristsirge pikkuseks pool antud lõigu pikkust ehk d÷2. Tähistame ristlõigu teise otspunkti tähega N.
Joonis 4.B. Lõigul SN punkti K tuletamine	B. Ühendame punktid SN. Lahutame (graafiliselt) hüpotenuuslõigust SN lõigu LN pikkuse. Selleks asetame sirkli teraviku punkti N ning joonestame raadiusega LN kaare. Tähistame kaare lõikepunkti lõigul SN tähega K.
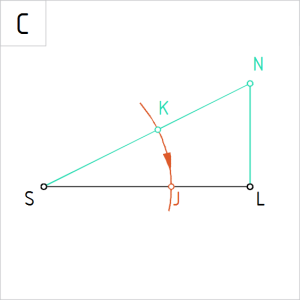Joonis 4.C. Lõigul SL punkti J tuletamine	C. Asetame sirkli teraviku punkti S ning joonestame raadiusega SK kaare lõikuma antud lõiguga SL. Kaare lõikepunkti antud lõigul tähistame tähega J.
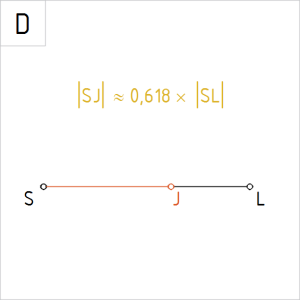Joonis 4.D. Punkt J jaotab sirglõigu SL kuldlõikes	D. Korrastame joonise. Punkt J jaotab sirglõigu SL kuldlõikes.Sirglõik \|SL\| on jaotatud kuldlõikes, kui punkt J jaotab lõigu kaheks osaks nii, et kogu lõigu suhe suuremasse osalõiku on sama mis suurema osalõigu suhe väiksemasse osalõiku.\|SL\|÷\|SJ\| = \|SJ\|÷\|JL\| Loe: \|SL\| – lõigu SL pikkus