Alljärgnevaid lauseid elementaargeomeetriast vajame kujutava geomeetria teadmiste ülesehitamisel ja ülesannete lahendamisel:

(1) Kaks sirgjoont, mis on paralleelsed kolmandaga, on paralleelsed ka omavahel.

(2) Kui paralleelsed sirged lõikavad nurga haarasid, siis lõigud, milleks paralleelid jaotavad nurga ühe haara, on võrdelised lõikudega, milleks nad jaotavad nurga teise haara.

(3) Sirgjoon ja tasand on paralleelsed, kui tasandil leidub antud sirgega paralleelne sirge.

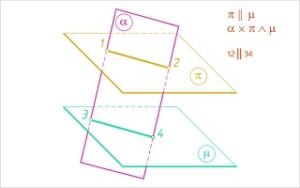
(4) Kaks tasandit on paralleelsed, kui ühe tasandi kahel lõikuval sirgel on kummalgi oma paralleel teisel tasandil.

(5) Sirgjoon ja tasand on teineteisega risti, kui tasandil leidub kaks lõikuvat sirget, mis on risti antud sirgega.

(6) Kaks tasandit, mis on paralleelsed kolmandaga, on paralleelsed ka omavahel.

(7) Paralleelsete tasandite lõikumisel tasandiga tekivad paralleelsed lõikesirged.

(8) Kolme tasandi lõikesirged on kas paralleelsed või lõikuvad kõik ühes punktis.

(9) Tasandi normaal (ristsirge) on risti iga sirgega, mis asetseb sellel tasandil.

(10) Igast punktist saab läbi panna üheainsa sirge, mis on risti antud tasandiga.

(11) Igast punktist saab läbi panna üheainsa tasandi, mis on risti antud sirgega.

(12) Iga tasand, mis läbib antud tasandi normaali, on selle antud tasandiga risti.

(13) Kui sirge pole risti antud tasandiga, siis saab temast läbi panna üheainsa tasandi, mis on antud tasandiga risti. Selle risttasandi määrab antud sirge koos tasandi iga normaaliga, mis antud sirget lõikab.

(14) Kahe kiivsirge vahelist nurka mõõdetakse tavalise nurgaga, mille haarad on nende kiivsirgetega paralleelsed.

(15) Kahetahulist nurka mõõdetakse nurgaga, mille haarad asetsevad teine teisel tahul ning on risti tahkude lõikejoonega (kahetahulise nurga servaga). Kahetahulist nurka võib aga mõõta ka nurgaga nende tahkude normaalide vahel.

Allikas: Kujutav geomeetria. O.Rünk, N.Paluver, A.Talvik – Tln, 1986

Tutvu meie kursuste ja blogiartiklitega.